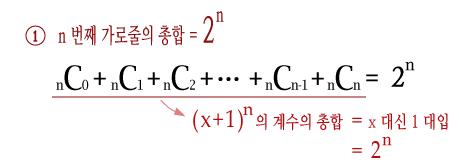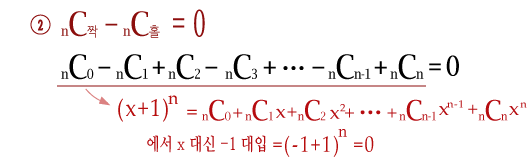문제
자연수 과 정수 가 주어졌을 때 이항 계수 를 구하는 프로그램을 작성하시오.
입력
첫째 줄에 과 가 주어진다. (1 ≤ ≤ 10, 0 ≤ ≤ )
출력
를 출력한다.
예제 입력
5 2
예제 출력
10
힌트
출처
- 문제를 만든 사람: baekjoon
이항계수 구하기는 재귀 프로그래밍의 기초이다.
이항계수란 n개의 원소에서 r개의 원소를 뽑아내는 방법의 수를 나타낸다.
즉, nCr과 같이 수학에서 조합을 뜻한다.
이항계수 프로그래밍의 해법은
nCr = n-1Cr-1 + n-1Cr의 공식으로 이루어진다.
무슨 의미냐면
n개의 원소 중 r개의 원소를 뽑아내는 경우의 수는 맨 마지막 원소 n을 제외한
n-1개의 원소 중 r-1개를 뽑아내는 경우의 수
+
n-1개의 원소 중 r개를 뽑아내는 경우의 수
의 합이다.
즉, 이미 n번째 원소를 선택했다고 가정하고 나머지 원소 중에서 r-1개를 뽑는 것과
n번째 원소를 제외한 나머지 중에서 r개의 원소를 뽑는 경우의 합이다.
import java.util.Scanner; public class Main { public static void main(String[] args) { Scanner sc = new Scanner(System.in); int N = sc.nextInt(); int K = sc.nextInt(); sc.close(); int result = calc(N, K); System.out.println(result); } /* 이항 계수란: * N개의 원소를 가지는 집합에서 크기가 K인 부분집합을 고르는 경우의 수를 이항계수라고 한다. */ public static int calc(int N, int K){ if(N == K || K == 0) return 1; /* N개의 원소 중에서 K개의 원소를 뽑아내는 경우의 수는 * N - 1 개의 원소 중 K - 1 개의 원소를 뽑는 경우와 N - 1 개의 원소 중 K 개의 원소를 뽑는 경우의 수의 합이다. * N - 1 개의 원소 중 K - 1 개의 원소는 뽑는 경우란, N번째 원소를 선택하고 나머지 원소 중 나머지 원소 중 나머지를 선택하는 경우의 수이고 * N - 1 개의 원소 중 K 개의 원소를 뽑는 경우란, N번째 원소를 선택하지 않고 나머지 원소 중 나머지를 선택하는 경우이다. * 즉, N 개의 원소 중에서 K 개의 원소를 뽑아내는 경우의 수란 * N 개의 원소 중 N번째 원소를 선택하고 나머지를 뽑는 경우와 N번째 원소를 선택하지 않고 나머지를 뽑는 경우의 합이다. */ return calc(N - 1, K - 1) + calc(N - 1, K); } }
이항 계수의 공식을 좀더 깊게 알아보기:
이번 포스트에서 살펴볼 내용은 파스칼의 삼각형을 이용한 이항계수의 성질입니다.
이름은 파스칼의 삼각형입니다만, 실제로는 파스칼이 유럽에 소개한 것보다 몇백 년 전에 아라비아나 중국에서는 이미 널리 알려져 있었다고 합니다. 파스칼은 이것을 정리해서 자신의 논문에서 소개한 거고요. 이런 이유로 "파스칼의 삼각형" 이 아니라 "산술 삼각형"이라고 부르기도 하는 모양입니다만, 누가 먼저냐가 우리의 주된 관심사는 아니므로 그냥 그런가 보다 하기로 해두죠.
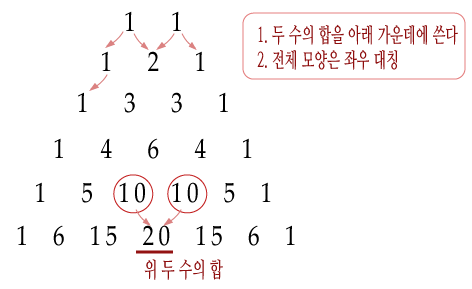
일단 전체적인 모양을 보기로 합시다.
규칙은 간단합니다. 맨 윗줄에 두 개의 1을 써두고 아래로 내려가면서 두 수의 합을 계속 적어가는 겁니다. 양쪽 끝은 더하는 수가 1 하나 뿐이므로 계속 1만 써 내려가는 거고요.
숫자로 이루어진 저 간단한 모양안에 정수의 여러 가지 재미(?) 있는 수학적 성질이 들어있지만, 일단은 전체적인 모양과 좌우대칭 형태로 이루어져 있다는 것만 기억해두기로 하고, 차근차근, 천천히 살펴보기로 하겠습니다.
먼저, n 번째 줄의 숫자들은 (x+1)^n 을 전개한 식의 계수들만 정리한 것입니다.
그림에서는 (x+1)^n 의 전개식을 오름차순으로 정리했습니다만, 오름차순이든 내림차순이든 숫자는 똑같습니다. 굳이 익숙하지 않은 오름차순으로 정리한 이유는 조합과 연결하기 쉽도록 하려는 나름의 배려입니다.
이제, 이항정리에서 각 항의 계수는 nCr 의 형태로 쓸 수 있으므로 nCr 을 이용하여 다시 표현해보도록 하겠습니다.
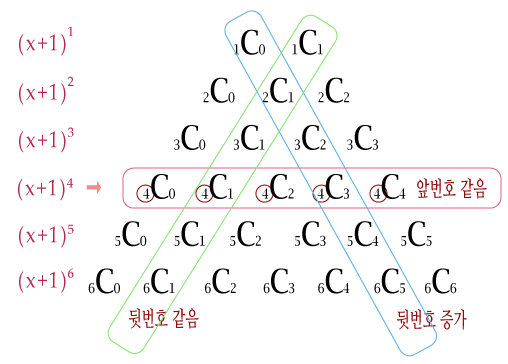
정리해 놓고 보면 위 그림처럼
① n 번째 줄은 nC0 부터 nCn 까지 n+1 개를 늘어놓은 것이므로 nCr 의 앞번호 n이 같습니다.
② ↙ 방향으로는 차수가 같은 항 들이므로 nCr 의 뒷번호 r 이 똑같습니다.
③ ↘ 방향으로는 차수가 하나씩 증가하게 되므로 nCr 의 뒷번호 r 이 증가합니다.
조합으로 표현된 파스칼 삼각형의 생성 규칙을 이해하셨나요?
그렇다면 파스칼의 삼각형을 이용한 조합의 성질 몇 가지를 먼저 살펴보도록 합시다.
위 그림은 이전 포스트에서 이미 한번 언급했던 내용입니다.
두 수의 합을 아래 가운데에 쓴다는 것이 파스칼삼각형의 기본이었으므로 nCr 과 nCr+1 의 합을 두 수의 아래 가운데에 적게 되고 그 값은 n+1Cr+1 이 된다는 거죠.
이것을 연속적으로 사용하는 것이 빗변 방향으로의 합에 관한 성질입니다.
더해지는 모양이 마치 하키스틱을 연상시킨다고 해서 흔히 "하키스틱" 이라고 불리기도 합니다.
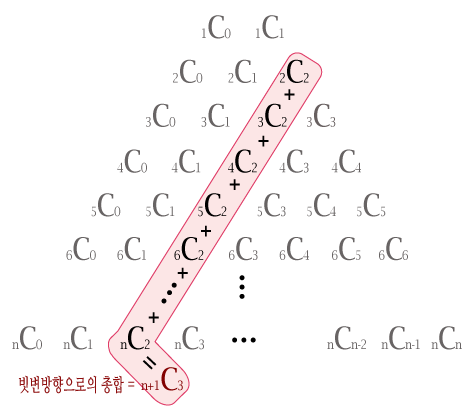
아래 그림처럼 빗변 ↙ 방향으로 rCr 부터 nCr 까지 더한 값은 n+1Cr+1 이 되고,
빗변 ↘ 방향으로 rC0 부터 nCr 까지 더한 값은 n+1Cr 이 된다는 성질입니다.
말로 하니까 어려운 것 같죠? 아래 그림을 보고 이해해보도록 합시다.
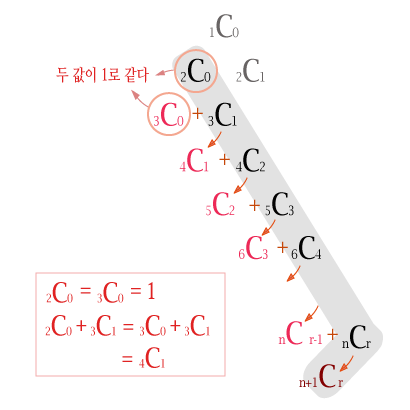
예를 들어, 2C2부터 시작해서 ↙ 방향으로 nC2 까지 다 더한 값이 n+1C3 이 된다는 건데, 원리는 간단합니다.
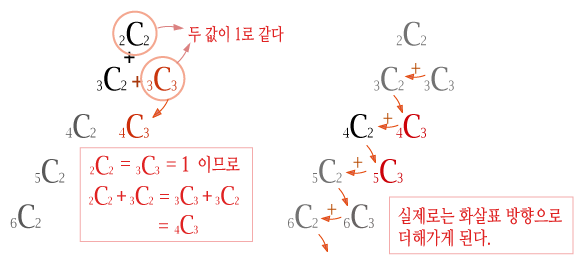
위쪽부터 차근차근 더해보도록 합시다. 먼저 2C2+3C2 를 계산할 건데, 우연히도 2C2 = 3C3 =1 입니다. 따라서, 2C2+3C2= 3C2+3C3 이 성립하고, 나란히 있는 두 수 3C2 과 3C3 의 합은 파스칼 삼각형 생성원리에 따라 4C3 이 됩니다. 거기에 다시 4C2를 더하면 4C2 + 4C3 = 5C3 이 되고, 거기에 다시 5C2 를 더하면 5C2 + 5C3 = 6C3 ... 이것을 계속해서 nC2 까지 더하면 결국 계산 결과는 n+1C3 이 됩니다. 결국, 가장 먼저 더하려는 2C2 를 같은 값을 갖는 3C3 으로 돌려서 더하고, 옆에 있는 수끼리 더한 값이 아래 가운데에 있는 값이 된다는 기본 생성원리로 쭈~욱 더하는 겁니다.
↘ 방향의 합도 마찬가지입니다.
아래 그림처럼 2C0 +3C1 + 4C2 + … + nCr 를 더할 때 2C0 + 3C1 의 계산에서 2C0 과 같은 값을 갖는 3C0 을 대신 더해서 3C0 + 3C1 = 4C1 을 얻게 되고, 그 뒤로는 옆의 수와 더해서 아래 가운데로 내려오는 기본 생성원리를 반복해서 적용하는 겁니다.
여기서 주의할 것은 처음에 시작할 때 rC0 = r+1C0 = 1 또는 rCr = r+1Cr+1 = 1 임을 이용하여 처음 시작하는 수를 같은 값을 같는 옆에 있는 수로 돌려서 더하는 것이므로 하키스틱은 반드시 빗변의 수 rCr 에서 시작해서 ↙ 방향으로 더하거나 rC0 에서 시작해서 ↘ 방향으로 더해야만 한다는 것입니다.
시험문제에 나올 경우, 가끔 출제자가 의도적으로 빗변에서부터 더하지 않는 경우도 있으니 반드시 확인하셔야 함정에 빠지지 않습니다.
이제, 파스칼의 삼각형을 이용하여 고등학교 교과과정에 나오는 이항계수의 성질을 살펴보도록 하죠.
먼저, 가로줄의 합에 관련된 성질입니다.
n 번째 가로줄은 (x+1)^n 을 전개해서 그 계수들을 차례로 적은 것이었으므로,
① x에 1을 대입하면 계수의 총합이 구해지게 되고 그 값은 (1+1)^n = 2^n 입니다.
② x에 -1을 대입하면 x의 짝수제곱은 +1, x의 홀수제곱은 -1 이 되므로 +,- 가
교대로 나오게 되며 그 값은 (-1+1)^n =0 입니다.
파스칼 삼각형의 가로줄의 합에 관해 참고서 등에서 언급하는 성질은 이 이외에도 미분과 적분을 이용한 식이 두 개 더 있습니다만, 위 세 가지 성질에 비해서 상대적으로 출제 빈도가 낮으며, 특히 미분을 이용한 식은 이 포스트보다는 이항분포에서 살펴보는 것이 더 의미가 있을듯해서 다음으로 설명을 미루기로 하겠습니다. [출처] 파스칼의 삼각형과 이항계수의 성질|작성자 강쌤
파스칼의 삼각형은 고등학교 과정에서는 그 자체가 중요하다기보다는, 이항계수의 성질을 잘 이해할 수 있도록 하는 보조적인 수단 정도로 기억해두는 것이 좋습니다.
특히, 앞자리가 똑같은 조합의 합, nC0 + nC1 + nC2 + … 와 같은 경우 진짜로 일일이 계산하라는 것이 아니라 이항정리에서 계수들에 관련된 문제이고, 그것을 가장 쉽게 정리해놓은 것이 파스칼의 삼각형이다 라는 정도로 정리해두도록 합시다.
'알고리즘(Java) > 이항 계수' 카테고리의 다른 글
| 백준 11051 이항 계수 2 (0) | 2017.12.07 |
|---|